Note that this example here shows no real scientific application and its purpose was to generate the code’s logo.

  • We consider a Peridynamic simulation of Soft material using RNP Peridynamic model (Regularized Nonlinear Peridynamic) developed and studied in Lipton 2016 and Jha and Lipton 2018. RNP model is implemented in class RNPBond.

  • Units are SI units, e.g. length is in meter, mass is in kg, force is in N, and time is in second.

  • Elastic properties of material are as follows:

    • Shear modulus G = 35.2E+03 Pa
    • Poisson ratio $\nu$ = 0.25
    • Density $\rho$ = 1011.204 kg/$m^3$

  • Fracture properties of material are as follows:

    • Critical energy release rate $G_c$ = 9.998E+02 J/$m^2$

  • For above elastic properties and fracture properties, we can compute the parameters in Peridynamic material model. This has been described in detail in RNPBond::computeParameters.

  • We consider a triangular mesh for “NLM” logo. It is contained in the box [0, 2.75 m] x [0, 1.5 m].

  • Horizon is $\epsilon$ = 0.1 m and mesh size is h = 0.025 m.

  • Time domain

    • Final time T = 0.01
    • Time steps N = 50000
    • Output frequency of simulation data: N/100

  • Boundary condition

    • We apply body force along horizontal axis on whole material domain.

    • Force is given by $f_x(x,y,t) = f t sin(n\pi x/L_x)$ where n = 3 and f = 1.5E+09.

  • We specify Displacement, Velocity, Force and Damage_Z as output candidates.

The complete YAML configuration file is available here.

Mesh

We obtain mesh using Gmsh library with mesh size h = 0.025.

setup

Results

We show damage plot at time t = 0.008, 0.009, 0.01 seconds.

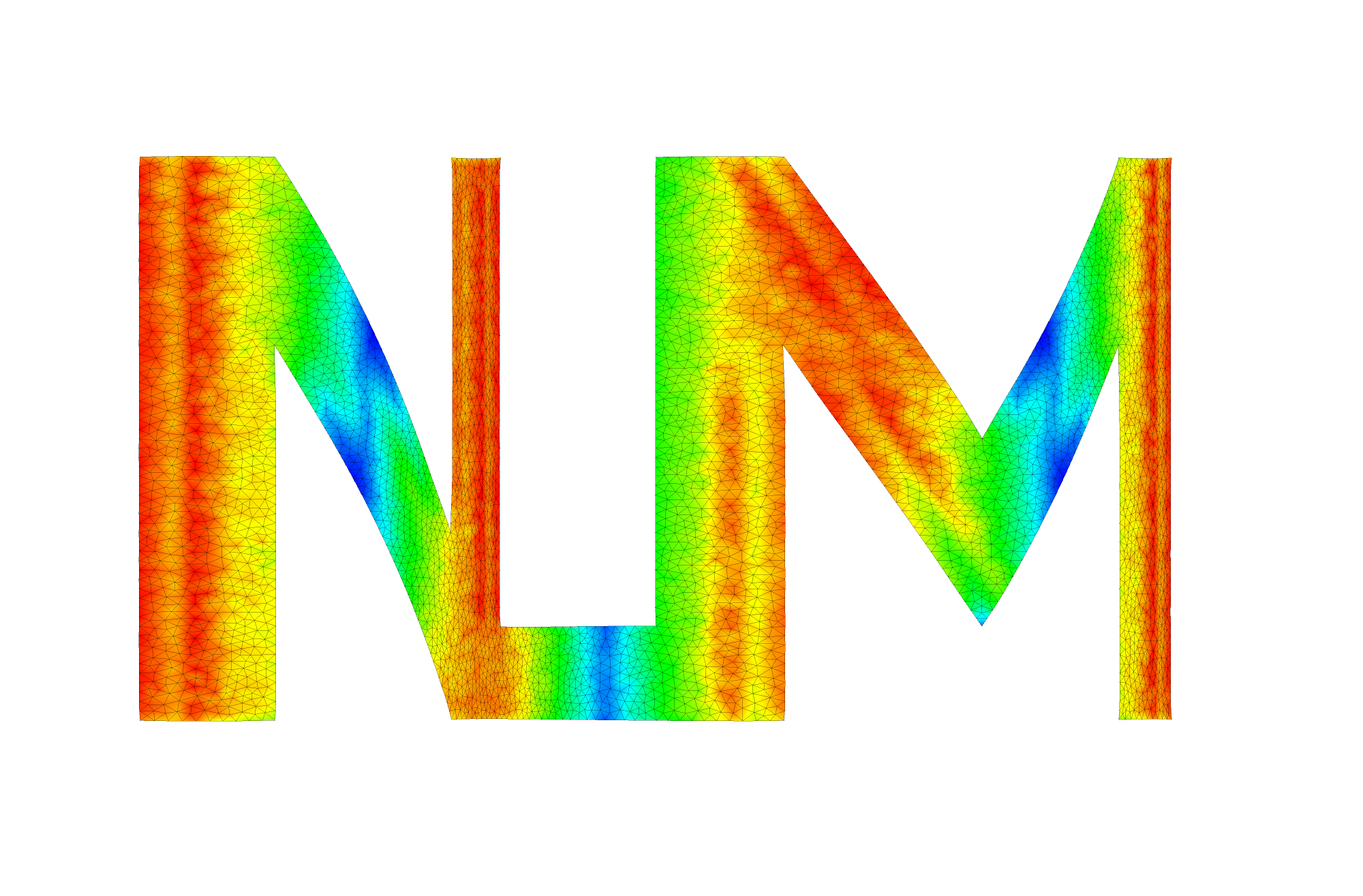
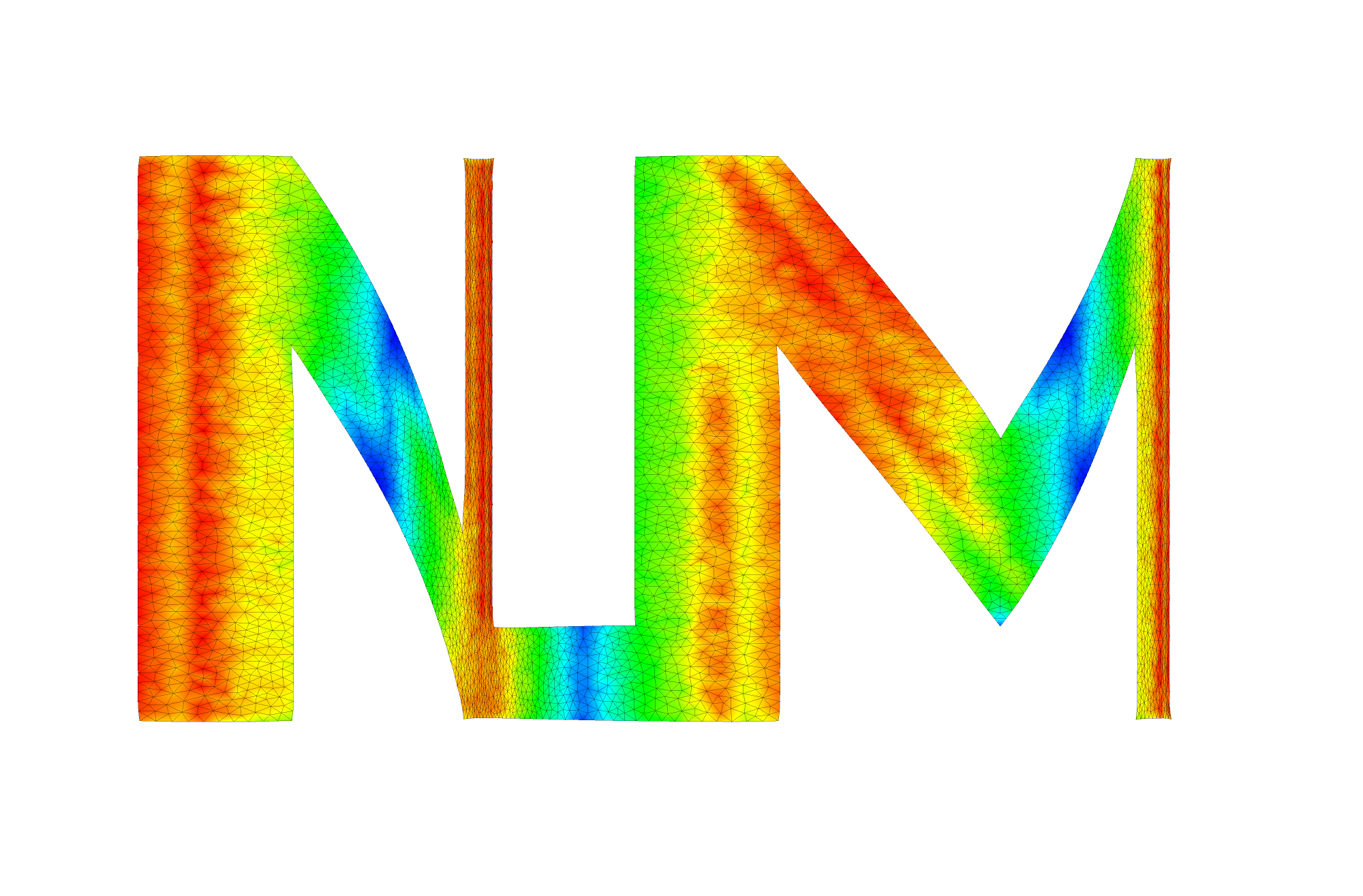
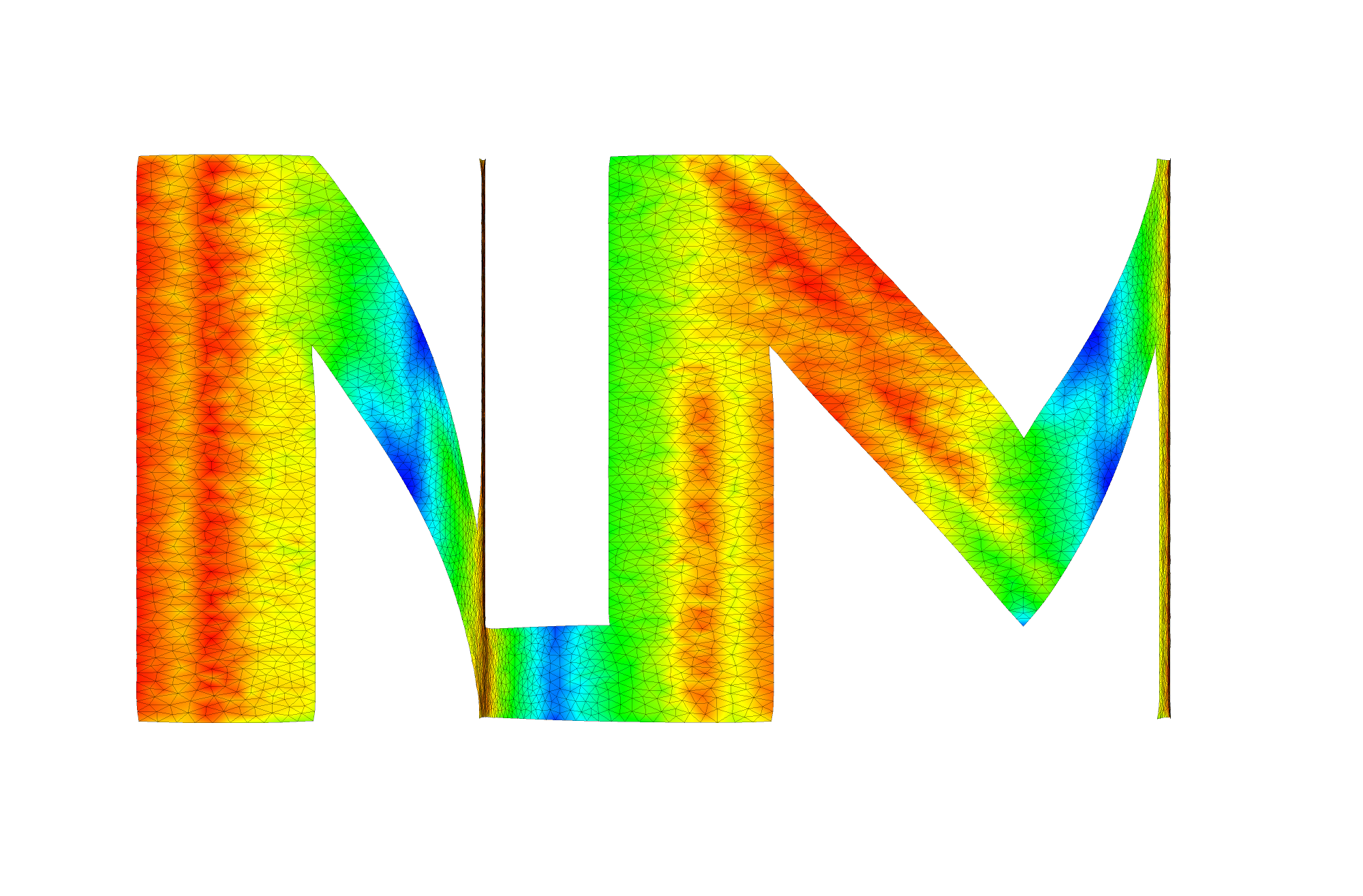
setup

setup

setup

Video of simulation: