A base class which provides methods to map points to/from reference element and to compute quadrature data. More...

#include <baseElem.h>

Inheritance diagram for fe::BaseElem:

Collaboration diagram for fe::BaseElem:

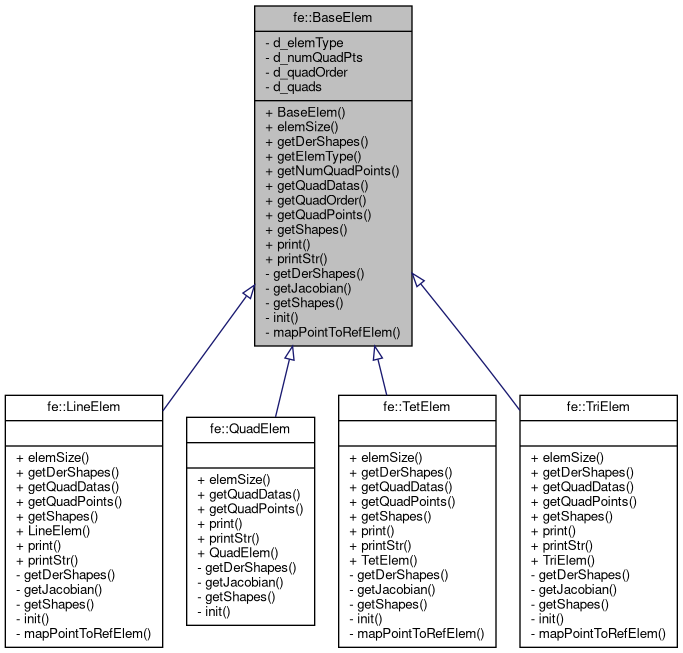
Public Member Functions
	BaseElem (size_t order, size_t element_type)
	Constructor. More...

virtual double	elemSize (const std::vector< util::Point3 > &nodes)=0
	Returns the size of element (length in 1-d, area in 2-d, volume in 3-d element) More...

virtual std::vector< std::vector< double > >	getDerShapes (const util::Point3 &p, const std::vector< util::Point3 > &nodes)
	Returns the values of derivative of shape function at point p. More...

size_t	getElemType ()
	Get element type. More...

size_t	getNumQuadPoints ()
	Get number of quadrature points in the data. More...

virtual std::vector< fe::QuadData >	getQuadDatas (const std::vector< util::Point3 > &nodes)=0
	Get vector of quadrature data. More...

size_t	getQuadOrder ()
	Get order of quadrature approximation. More...

virtual std::vector< fe::QuadData >	getQuadPoints (const std::vector< util::Point3 > &nodes)=0
	Get vector of quadrature data. More...

virtual std::vector< double >	getShapes (const util::Point3 &p, const std::vector< util::Point3 > &nodes)
	Returns the values of shape function at point p. More...

void	print (int nt=0, int lvl=0) const
	Prints the information about the instance of the object. More...

std::string	printStr (int nt=0, int lvl=0) const
	Returns the string containing information about the instance of the object. More...

Private Member Functions
virtual std::vector< std::vector< double > >	getDerShapes (const util::Point3 &p)=0
	Returns the values of derivative of shape function at point p on reference element. More...

virtual double	getJacobian (const util::Point3 &p, const std::vector< util::Point3 > &nodes, std::vector< std::vector< double >> *J)=0
	Computes Jacobian of map from reference element to given element . More...

virtual std::vector< double >	getShapes (const util::Point3 &p)=0
	Returns the values of shape function at point p on reference element. More...

virtual void	init ()=0
	Compute the quadrature points. More...

virtual util::Point3	mapPointToRefElem (const util::Point3 &p, const std::vector< util::Point3 > &nodes)
	Maps point p in a given element to the reference element and returns the mapped point. More...

Private Attributes
size_t	d_elemType
	Element type.

size_t	d_numQuadPts
	Number of quadrature points for order d_quadOrder.

size_t	d_quadOrder
	Order of quadrature point integration approximation.

std::vector< fe::QuadData >	d_quads
	Quadrature data collection.

Detailed Description

A base class which provides methods to map points to/from reference element and to compute quadrature data.

At present, all types of element employ isoparametric mapping to map points on reference element to any other element of same type.

For any type of element, such as fe::LineElem, fe::TriElem, fe::QuadElem, we have following important points

A simple element with predefined vertices is considered as a reference element . E.g., reference element in fe::TriElem is a triangle with vertices at .
Points in reference element are described by $(\xi, \eta, \zeta)$ (in 3-d), $(\xi, \eta)$ (in 2-d), and $\xi$ (in 1-d). Points in any other element are described by (in 3-d), (in 2-d), and (in 1-d). Here, we restrict discussion to 3-d element. For 2-d, one should ignore coordinate $\zeta$ and , and for 1-d, one should ignore $\eta, \zeta$ and .
Associated to vertices of the element we have shape functions , where is the number of vertices in the element. Shape functions are functions of point $(\xi, \eta, \zeta) \in T^0$ . For each type of element, is fixed.
For any element , shape functions are denoted as and are functions of point $(x,y,z) \in T$ .
Element is described by vertices .
A map $\Phi : T^0 \to T$ , where is a given element formed by vertices , is defined as follows:
$x(\xi, \eta, \zeta) = \sum_{i=1}^n N^0_i(\xi, \eta, \zeta) v^i_x, \quad y(\xi, \eta, \zeta) = \sum_{i=1}^n N^0_i(\xi, \eta, \zeta) v^i_y, \quad z (\xi, \eta, \zeta) = \sum_{i=1}^n N^0_i(\xi, \eta, \zeta) v^i_z$
where are the x, y, and z component of point .
Jacobian of map $\Phi : T^0 \to T$ is given by
$J = \left[ { \begin{array}{ccc} \frac{dx}{d\xi} &\frac{dy}{d\xi} & \frac{dz}{d\xi} \\ \frac{dx}{d\eta} & \frac{dy}{d\eta} & \frac{dz}{d\eta} \\ \frac{dx}{d\zeta} & \frac{dy}{d\zeta} & \frac{dz}{d\zeta} \\ \end{array} } \right].$
For 2-d element it is
$J = \left[ { \begin{array}{cc} \frac{dx}{d\xi} &\frac{dy}{d\xi} \\ \frac{dx}{d\eta} & \frac{dy}{d\eta} \\ \end{array} } \right].$
For 1-d element it is
$J = \frac{dx}{d\xi}.$
Determinant of the Jacobian is an important quantity and is used to compute the quadrature points, and inverse map $\Phi^{-1} : T \to T^0$ .

See also: fe::LineElem, fe::TriElem, fe::QuadElem

Constructor & Destructor Documentation

◆ BaseElem()

fe::BaseElem::BaseElem	(	size_t	order,
		size_t	element_type
	)

Constructor.

Parameters

order	Order of quadrature point approximation
element_type	Type of element

Member Function Documentation

◆ elemSize()

virtual double fe::BaseElem::elemSize ( const std::vector< util::Point3 > & nodes )

pure virtual

Returns the size of element (length in 1-d, area in 2-d, volume in 3-d element)

Parameters

nodes Vertices of element

Returns: size Size of the element

Implemented in fe::TriElem, fe::TetElem, fe::QuadElem, and fe::LineElem.

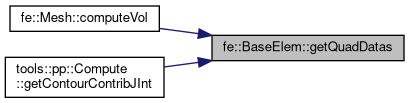
Referenced by fe::Mesh::computeVol().

Here is the caller graph for this function:

◆ getDerShapes() [1/2]

virtual std::vector<std::vector<double> > fe::BaseElem::getDerShapes ( const util::Point3 & p )

privatepure virtual

Returns the values of derivative of shape function at point p on reference element.

Parameters

p	Location of point

Returns: vector Vector of derivative of shape functions

Implemented in fe::TriElem, fe::TetElem, fe::QuadElem, and fe::LineElem.

◆ getDerShapes() [2/2]

std::vector< std::vector< double > > fe::BaseElem::getDerShapes	(	const util::Point3 &	p,
		const std::vector< util::Point3 > &	nodes
	)

virtual

Returns the values of derivative of shape function at point p.

Parameters

p	Location of point
nodes	Vertices of element

Returns: vector Vector of derivative of shape functions

Reimplemented in fe::TriElem, fe::TetElem, and fe::LineElem.

◆ getElemType()

size_t fe::BaseElem::getElemType ( )

inline

Get element type.

Returns: type Type of element

◆ getJacobian()

virtual double fe::BaseElem::getJacobian	(	const util::Point3 &	p,
		const std::vector< util::Point3 > &	nodes,
		std::vector< std::vector< double >> *	J
	)

privatepure virtual

Computes Jacobian of map from reference element $ T^0 $ to given element $ T $ .

Parameters

p	Location of point in reference element
nodes	Vertices of element
J	Matrix to store the Jacobian

Returns: det(J) Determinant of the Jacobain

Implemented in fe::TriElem, fe::TetElem, fe::QuadElem, and fe::LineElem.

◆ getNumQuadPoints()

size_t fe::BaseElem::getNumQuadPoints ( )

inline

Get number of quadrature points in the data.

Returns: N Number of quadrature points

◆ getQuadDatas()

virtual std::vector<fe::QuadData> fe::BaseElem::getQuadDatas ( const std::vector< util::Point3 > & nodes )

pure virtual

Get vector of quadrature data.

Given element vertices, this method returns the list of quadrature point and associated quantities. Here, order of quadrature approximation and element type are set in the constructor. List of data for each quad point:

quad point
quad weight
shape function evaluated at quad point
derivative of shape function evaluated at quad point
Jacobian matrix
determinant of the Jacobian

Parameters

nodes Vector of vertices of an element

Returns: vector Vector of QuadData

Implemented in fe::TriElem, fe::TetElem, fe::QuadElem, and fe::LineElem.

Referenced by fe::Mesh::computeVol(), and tools::pp::Compute::getContourContribJInt().

Here is the caller graph for this function:

◆ getQuadOrder()

size_t fe::BaseElem::getQuadOrder ( )

inline

Get order of quadrature approximation.

Returns: order Order of approximation

◆ getQuadPoints()

virtual std::vector<fe::QuadData> fe::BaseElem::getQuadPoints ( const std::vector< util::Point3 > & nodes )

pure virtual

Get vector of quadrature data.

Given element vertices, this method returns the list of quadrature point and essential quantities at quadrature points. Here, order of quadrature approximation and element type are set in the constructor. List of data for each quad point:

quad point
quad weight
shape function evaluated at quad point

This function is a lite version of fe::BaseElem::getQuadDatas.

Parameters

nodes Vector of vertices of an element

Returns: vector Vector of QuadData

Implemented in fe::TriElem, fe::TetElem, fe::QuadElem, and fe::LineElem.

◆ getShapes() [1/2]

virtual std::vector<double> fe::BaseElem::getShapes ( const util::Point3 & p )

privatepure virtual

Returns the values of shape function at point p on reference element.

Parameters

p	Location of point

Returns: vector Vector of shape functions at point p

Implemented in fe::TriElem, fe::TetElem, fe::QuadElem, and fe::LineElem.

◆ getShapes() [2/2]

std::vector< double > fe::BaseElem::getShapes	(	const util::Point3 &	p,
		const std::vector< util::Point3 > &	nodes
	)

virtual

Returns the values of shape function at point p.

The point p is assumed to be inside an element $ T$ given by nodes. The idea is to first map point p to the point $ p^0$ in reference element $ T^0 $ and then compute shape functions at $ p^0 $ .

The map from any element $ T $ to reference element is $ T^0 $ gets complex for elements like fe::QuadElem. For elements fe:LineElem and fe::TriElem, this is simple to compute. Therefore, this method is only implemented for fe::TriElem and fe::LineElem.

Parameters

p	Location of point
nodes	Vertices of element

Returns: vector Vector of shape functions at point p

Reimplemented in fe::TriElem, fe::TetElem, and fe::LineElem.

◆ init()

void fe::BaseElem::init ( )

privatepure virtual

Compute the quadrature points.

This must be implemented by inheriting classes.

Implemented in fe::TriElem, fe::TetElem, fe::QuadElem, and fe::LineElem.

◆ mapPointToRefElem()

util::Point3 fe::BaseElem::mapPointToRefElem	(	const util::Point3 &	p,
		const std::vector< util::Point3 > &	nodes
	)

privatevirtual

Maps point p in a given element to the reference element and returns the mapped point.

Parameters

p	Location of point
nodes	Vertices of element

Returns: vector Vector of shape functions at point p

Reimplemented in fe::TriElem, fe::TetElem, and fe::LineElem.

◆ print()

void fe::BaseElem::print	(	int	nt = `0`,
		int	lvl = `0`
	)		const

inline

Prints the information about the instance of the object.

Parameters

nt	Number of tabs to append before each line of string
lvl	Level of information sought (higher level means more information)

Here is the call graph for this function:

◆ printStr()

std::string fe::BaseElem::printStr	(	int	nt = `0`,
		int	lvl = `0`
	)		const

Returns the string containing information about the instance of the object.

Parameters

nt	Number of tabs to append before each line of string
lvl	Level of information sought (higher level means more information)

Returns: string String containing information about this object

Referenced by print().

Here is the call graph for this function:

Here is the caller graph for this function:

The documentation for this class was generated from the following files:

/root/project/src/fe/baseElem.h
/root/project/src/fe/baseElem.cpp

Public Member Functions

Private Member Functions

Private Attributes

Detailed Description

Constructor & Destructor Documentation

◆ BaseElem()

Member Function Documentation

◆ elemSize()

◆ getDerShapes() [1/2]

◆ getDerShapes() [2/2]

◆ getElemType()

◆ getJacobian()

◆ getNumQuadPoints()

◆ getQuadDatas()

◆ getQuadOrder()

◆ getQuadPoints()

◆ getShapes() [1/2]

◆ getShapes() [2/2]

◆ init()

◆ mapPointToRefElem()

◆ print()

◆ printStr()