NLMech  0.1.0
Public Member Functions | Private Attributes
tools::pp::Compute Class Reference

Processes simulation results and computes post-processing quantities. More...

#include <compute.h>

Collaboration diagram for tools::pp::Compute:
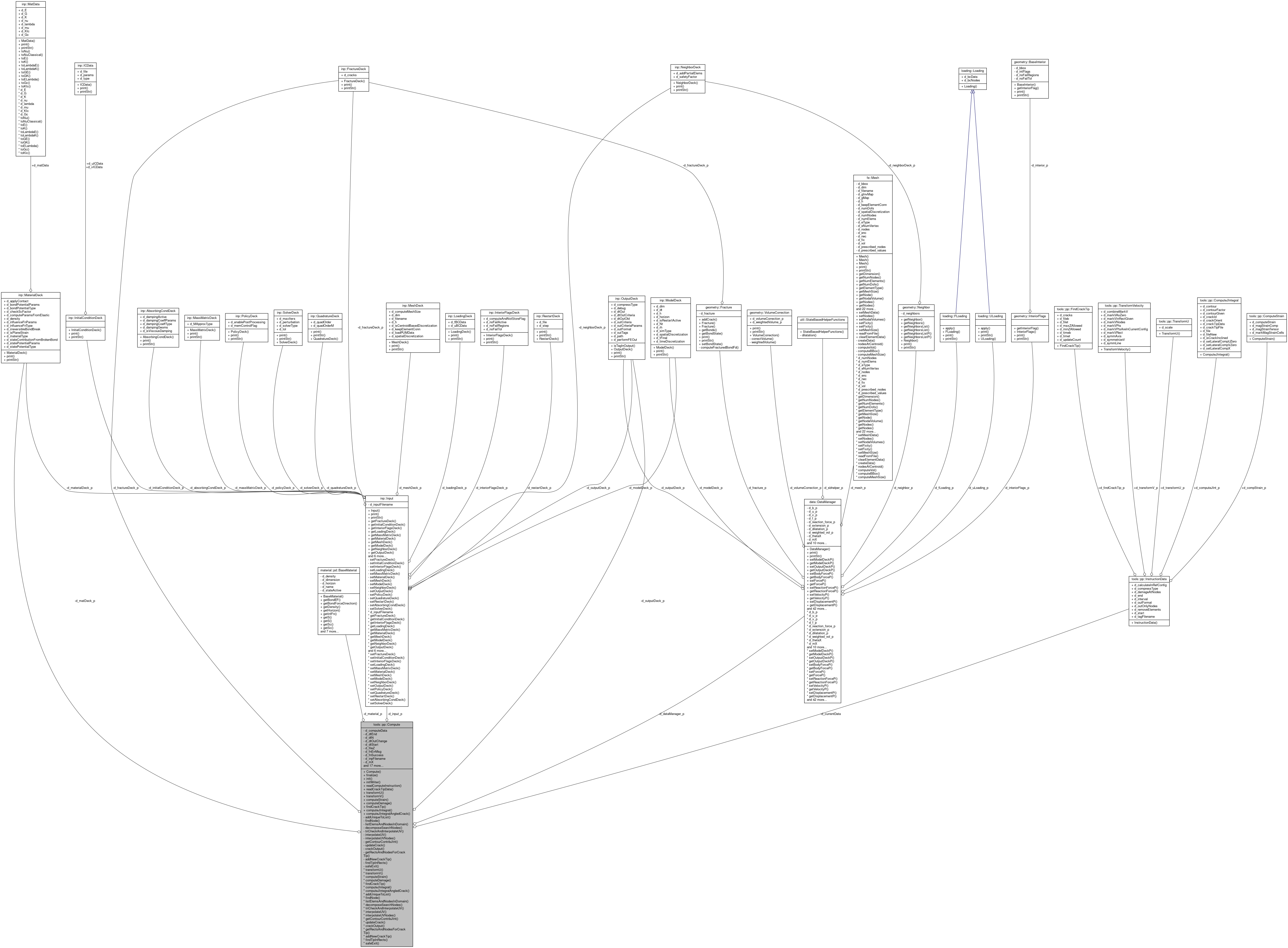
Collaboration graph

Public Member Functions

 Compute (const std::string &filename)
 Constructor. More...
 
void finalize ()
 Finalize.
 
void init ()
 Initialize the class based on input data.
 
void initWriter (rw::writer::Writer *writer, std::vector< util::Point3 > *u)
 Create new writer object if it is not already done so. More...
 
void readComputeInstruction (const std::string &set, tools::pp::InstructionData *data)
 Read compute instruction. More...
 
void readCrackTipData (const std::string &filename, int crack_id, std::vector< tools::pp::CrackTipData > *data, bool is_inclined=false)
 Read crack tip data. More...
 
Post-processing methods
void transformU (rw::writer::Writer *writer)
 Transform displacement. More...
 
void transformV (rw::writer::Writer *writer)
 Transform velocity. More...
 
void computeStrain (rw::writer::Writer *writer)
 Compute strain and stress. More...
 
void computeDamage (rw::writer::Writer *writer, std::vector< double > *Z, bool perf_out=false)
 Compute damage at nodes. More...
 
void findCrackTip (std::vector< double > *Z, rw::writer::Writer *writer)
 Find crack tip location and velocity. More...
 
void computeJIntegral ()
 Compute J integral. More...
 
void computeJIntegralAngledCrack ()
 Compute J integral where crack line is angled as opposed to either horizontal or verticle line.
 

Private Member Functions

Utility methods
void addUniqueToList (size_t i, std::vector< size_t > *list)
 Inserts element to list if not present. More...
 
size_t findNode (const util::Point3 &x, const std::vector< util::Point3 > *nodes, const std::vector< util::Point3 > *u=nullptr)
 Find node closest to given point. More...
 
void listElemsAndNodesInDomain (const std::pair< util::Point3, util::Point3 > &cd, const double &tol, const double &tol_elem, std::vector< size_t > *nodes, std::vector< size_t > *elements, bool calc_in_ref)
 Find node within contour and elements intersecting contour. More...
 
void decomposeSearchNodes (const std::pair< util::Point3, util::Point3 > &cd, std::vector< size_t > *nodes, std::vector< size_t > *nodes_new)
 Decompose node list into two lists. More...
 
bool triCheckAndInterpolateUV (const util::Point3 &p, util::Point3 &up, util::Point3 &vp, const std::vector< size_t > &ids, bool calc_in_ref, bool check_only=false)
 Interpolates displacement and velocity at given point in triangle. More...
 
void interpolateUV (const util::Point3 &p, util::Point3 &up, util::Point3 &vp, const std::vector< size_t > *nodes, const std::vector< size_t > *elements, bool calc_in_ref)
 Interpolates displacement and velocity at given point. More...
 
size_t interpolateUVNodes (const util::Point3 &p, util::Point3 &up, util::Point3 &vp, const std::vector< size_t > *nodes, bool calc_in_ref)
 
void getContourContribJInt (const util::Point3 &p, const std::vector< size_t > *nodes, const std::vector< size_t > *elements, const util::Point3 &normal, double &pd_energy, double &kinetic_energy, double &elastic_energy, util::Point3 &dot_u, bool calc_in_ref, const tools::pp::CrackTipData &ctip)
 Computes contribution to energy into crack from the quadrature point on contour. More...
 
void updateCrack (const double &time, const std::vector< double > *Z)
 Updates crack tip location and crack velocity. More...
 
void crackOutput ()
 Performs output of crack tip data.
 
void getRectsAndNodesForCrackTip (inp::EdgeCrack &crack, std::vector< std::pair< util::Point3, util::Point3 >> &rects_t, std::vector< std::pair< util::Point3, util::Point3 >> &rects_b, std::vector< std::vector< size_t >> &nodes_t, std::vector< std::vector< size_t >> &nodes_b, std::vector< std::vector< double >> &Z_t, std::vector< std::vector< double >> &Z_b, const std::vector< double > *Z)
 Creates sequence of rectangles for crack tip search, and finds the ids of nodes in each rectangle and damage associated to the node. More...
 
void addNewCrackTip (inp::EdgeCrack &crack, util::Point3 pnew, double time, bool is_top)
 Adds new tip to crack, computes velocity and crack length. More...
 
util::Point3 findTipInRects (inp::EdgeCrack &crack, const double &max_Z, const std::vector< std::pair< util::Point3, util::Point3 >> &rects, const std::vector< std::vector< size_t >> &nodes, const std::vector< std::vector< double >> &Zs, const std::vector< double > *Z, bool is_top)
 Finds new crack tip location from the rectangle data. More...
 
void safeExit (const std::string &err_message, rw::writer::Writer *writer=nullptr)
 Exits code safely in the event there is error. More...
 

Private Attributes

std::vector< tools::pp::InstructionData > d_computeData
 List of compute sets.
 
tools::pp::InstructionData * d_currentData
 Current active compute data.
 
data::DataManager * d_dataManager_p
 Pointer to the Data Mananger.
 
size_t d_dtEnd
 Global output start step. Default is maximum output step for the simulation, i.e. d_dtN.
 
size_t d_dtN
 Total number of output files to process.
 
size_t d_dtOutChange
 Time step at which output interval changes. More...
 
size_t d_dtStart
 Global output start step. Default is 1.
 
std::string d_fileZ
 Filename (if any) to read damage at nodes.
 
std::string d_fnErrMsg
 
bool d_fnSuccess
 Save success/failur of function.
 
inp::FractureDeck * d_fractureDeck_p
 Fracture deck.
 
std::string d_inpFilename
 Input filename for compute instruction.
 
inp::Input * d_input_p
 Pointer to Fracture object. More...
 
inp::MaterialDeck * d_matDeck_p
 Material deck.
 
material::pd::BaseMaterial * d_material_p
 Pointer to Material object.
 
std::vector< double > d_mX
 Weighted volume. More...
 
size_t d_nC
 Current active compute set.
 
bool d_needDamageZ
 Need damage at nodes.
 
bool d_needNeighborList
 Need neighbor list.
 
int d_nOut
 Current active simulation output step.
 
std::string d_outFilename
 Current active output filename to save postprocessed data.
 
std::string d_outPath
 Output path where postprocessed files are created.
 
std::string d_outPreTag
 Initial tag for each post-processing output.
 
inp::OutputDeck * d_outputDeck_p
 Model deck. More...
 
std::string d_simInpFilename
 Simulation input filename. More...
 
std::string d_simOutFilename
 Mesh filename to get displacement and velocity (results of simulation)
 
std::string d_tagZ
 Tag of damage function Z in vtu file.
 
std::vector< double > d_thetaX
 Dilation. More...
 
double d_time
 Current time.
 
std::vector< util::Point3 > d_u
 Displacement of nodes.
 
bool d_uPlus
 Specify if we consider u(n+1) or u(n)
 
std::vector< util::Point3 > d_v
 Velocity of nodes.
 
bool d_writerReady
 State of writer class.
 
std::vector< double > d_Z
 Damage of nodes.
 

Detailed Description

Processes simulation results and computes post-processing quantities.

Currently we have implemented

  • Transformation of displacement data such as scaling of displacement by specified factor
  • Transformation of velocity data such as
    1. marking velocity of specified nodes as zero
    2. symmetries velocity with specified line of symmetry
  • Strain and stress calculation and magnitude of strain calculation
  • Finding crack tip location and crack tip velocity
  • Computation of nodal damage
  • Computation of J integral

Constructor & Destructor Documentation

◆ Compute()

tools::pp::Compute::Compute ( const std::string &  filename)
explicit

Constructor.

Parameters
filenameName of input (yaml) file
Here is the call graph for this function:

Member Function Documentation

◆ addNewCrackTip()

void tools::pp::Compute::addNewCrackTip ( inp::EdgeCrack &  crack,
util::Point3  pnew,
double  time,
bool  is_top 
)
private

Adds new tip to crack, computes velocity and crack length.

Parameters
crackCrack data which will be updated
pnewNew crack tip
timeTime of update
is_topTrue if this is top (right) tip otherwise false

◆ addUniqueToList()

void tools::pp::Compute::addUniqueToList ( size_t  i,
std::vector< size_t > *  list 
)
private

Inserts element to list if not present.

Parameters
iElement to be inserted
listPointer to list

◆ computeDamage()

void tools::pp::Compute::computeDamage ( rw::writer::Writer *  writer,
std::vector< double > *  Z,
bool  perf_out = false 
)

Compute damage at nodes.

We compute the damage function

\[ Z(x) := \sup_{y\in B_\epsilon(x)} \frac{|S(y,x;u)|}{S_c(y,x)}, \]

where $ B_\epsilon(x) $ is the ball centered at $ x$, $ S(y, x;u) $ is the bond-strain between points $y,x$, and $S_c(y,x) $ is the critical strain.

Parameters
writerPointer to vtk writer
ZPointer to nodal damage
perf_outFlag to perform output of damage data

Referenced by Compute().

Here is the caller graph for this function:

◆ computeJIntegral()

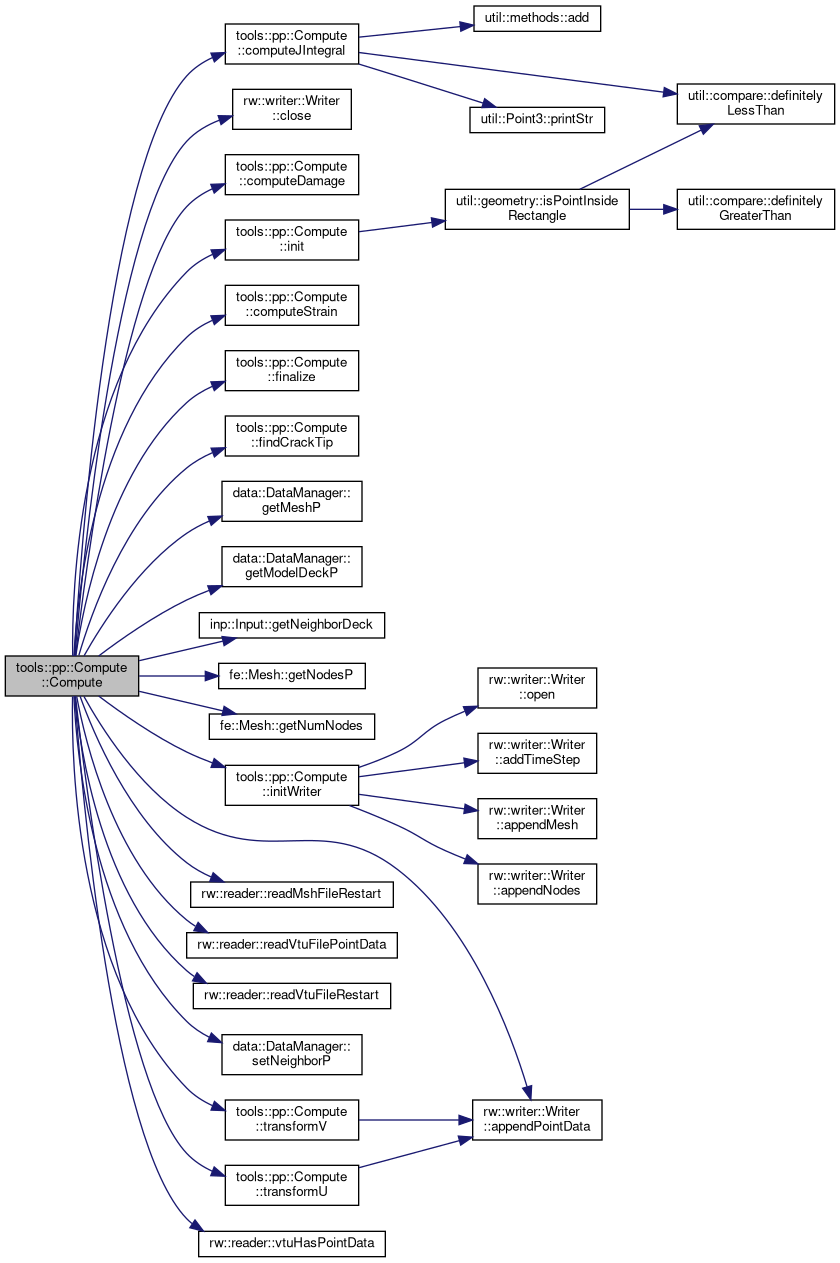
void tools::pp::Compute::computeJIntegral ( )

Compute J integral.

We consider rectangle near the crack tip and compute J-integral using the contour of rectangle. Schematic for horizontal crack (similar for vertical crack) 

                    D                    C
                    + + + + + + + + + + +
                    +                   +
                    +                   +
  ------------------+                   +
                    +                   +
                    +                   +
                    + + + + + + + + + + +
                   A                    B

Note: Contour is formed by lines A-B, B-C, C-D, D-A

Let contour is denoted as $ \Gamma(t) $, where $ t $ indicates contour moves with crack tip. Let domain inside contour is defined as $ A(t) $. Let the outward normal to the domain $ A(t) $ is $ n $, crack velocity direction is $ n_c$, and the crack velocity is $ v_c $. Since $ n_c$ is the crack velocity direction, we have crack velocity $ v_c = V n_c$, where $V $ is the magnitude of crack velocity.

We compute following seven kinds of energy associated to crack tip:

  1. Strain energy on contour:

    \[ E_{strain, \Gamma} := \int_{\Gamma(t)} \bar{W}(x) n \cdot n_c dx, \]

    where $ \bar{W}(x;u(t)) $ is the energy density at point $ x$ given by

    \[ \bar{W}(x;u(t)) = \frac{1}{|B_\epsilon(0)|} \int_{B_\epsilon(x)} |y-x| W(S(y,x;u(t))) dy.\]

    $ W(S(y,x;u)) $ is the pairwise energy density. For regularized bond based model (see material::pd::RNPBond), it is given by

    \[ W(S(y,x;u)) = J^\epsilon(|y-x|) \frac{1}{\epsilon |y-x|} \psi(|y-x| S(y,x;u)^2). \]

    From above we have

    \[\partial_S W(S(y,x;u)) = \frac{2J^\epsilon(|y-x|) S(y,x;u)}{\epsilon} \psi'(|y-x| S(y,x;u)^2). \]

    See material::pd::RNPBond for complete details about the material model.
  2. Strain energy rate on contour:

    \[ E_{strain rate, \Gamma} := \int_{\Gamma(t)}\bar{W}(x) n \cdot v_c dx = V E_{strain, \Gamma}, \]

    where $ V$ is the magnitude of crack velocity, $ v_c$ is the crack velocity.
  3. Kinetic energy rate on contour:

    \[ E_{kinetic rate, \Gamma} := \int_{\Gamma(t)} \frac{\rho}{2} |\dot{u}(x)|^2 n \cdot v_c dx, \]

    where $ \dot{u}(x)$ is velocity of material point $ x \in \Gamma (t) $.
  4. Elastic internal work rate on contour:

    \[ E_{elastic work rate, \Gamma} := \int_{\Gamma(t)} \frac{C}{2} [\nabla u (x) + \nabla u(x)^T]n \cdot \dot{u}(x) dx , \]

    where $ C $ is the elasticity tensor.
  5. Peridynamic internal work:

    \[ E_{pd work} = \frac{1}{|B_\epsilon(0)|} \int_{A^c(t)} \int_{A(t) \cap B_\epsilon(x)} \partial_S W(S(y,x; u(t))) \frac{y-x}{|y-x|} \cdot [(\nabla {u}(x,t) + \nabla {u}(y,t)) n_c] dy dx. \]

    Here $ W(S(y,x; u(t))) $ is the internal pairwise strain energy density as described above. $ \nabla u(x) n_c$ is the derivative of displacement along the crack velocity direction.
  6. Peridynamic internal work:

    \[ E_{pd work rate} = \frac{1}{|B_\epsilon(0)|} \int_{A^c(t)} \int_{A(t) \cap B_\epsilon(x)} \partial_S W(S(y,x; u(t))) \frac{y-x}{|y-x|} \cdot (\dot{u}(x,t) + \dot{u}(y,t)) dy dx. \]

  7. LEFM energy rate:

    \[ E_{lefm} = V G_c, \]

    where $ G_c$ is the critical energy release rate.
  8. Strain energy within contour domain:

    \[ E_{strain, A} = \int_{A(t)} W(x) dx. \]

  9. Kinetic energy within contour domain:

    \[ E_{kinetic, A} = \int_{A(t)} \frac{\rho}{2} |\dot{u}(x)|^2 dx. \]

  10. Peridynamic fracture energy:

    \[ E_{pd,fracture} = \int_{x, Z(x) > 1} \bar{W}(x;u(t)) dx \]

    where $ Z(x) $ is the damage at node x and $\bar{W}$ is the peridynamic energy density at point x.

Method:

  1. We store the ids of nodes which are within horizon distance from the contour. We also store the ids of elements which intersect the contour. All operations below are performed using this list of nodes and elements . This significantly reduces the computation as we no longer loop over whole list of nodes and elements.
  2. To compute

    \[ E(t) = \int_{\Gamma(t)} \left[ \frac{1}{2} \rho |\dot{u}(t)|^2 dt + \bar{W}(x; u(t)) \right] v\cdot n dx \]

    we discretize each edge in contour using 1-d line element. We use second order quadrature rule. We first find the displacement and velocity of the quadrature point using interpolation, see interpolateUV.
  3. At quadrature point, we compute peridynamic energy density using pdEnergy.

  4. To compute

    \[ \frac{2}{\epsilon |B_\epsilon(0)|} \int_{A^c(t)} \int_{A(t) \cap B_\epsilon(x)} \partial_S W(S(y,x; u(t))) \frac{y-x}{|y-x|} \cdot (\dot{u}(x,t) + \dot{u}(y,t)) dy dx \]

    we loop over nodes which are in complement of domain $A(t) $, i.e. $ A^c(t) $. We compute the contribution of each node in $ A^c(t) $ using pdForceWork.

    Todo:
    At present not computing $ E_{elastic work, \Gamma}$ as we require gradient of displacement along the normal to contour.
    Todo:
    At present not computing $ E_{pd internal work}$ as we require gradient of displacement at nodes.

Referenced by Compute().

Here is the call graph for this function:
Here is the caller graph for this function:

◆ computeStrain()

void tools::pp::Compute::computeStrain ( rw::writer::Writer *  writer)

Compute strain and stress.

We perform following post-processing calculation

  • compute strain and stress
  • compute magnitude (or absolute value of specified component of tensor) of strain tensor
  • mark strain of specified cells to given value
  1. Given an element $ T $ and its shape functions $ N_1, N_2,..., N_n $, the displacement at quadrature point is given by

    \[ u(x_q,y_q) = \sum_{i=1}^n N_i(x_q, y_q) u^i, \]

    where $ u^i $ is displacement of node $ i$. Linear strain is given by

    \[ E(x_q, y_q) = \franc{1}{2}( \nabla u(x_q, y_q) + \nabla u(x_q,y_q)^T ). \]

    Components of tensor are given by

    \[ E_{xx} = \frac{\partial u_x(x_q, y_q)}{\partial x}, \quad E_{yy} = \frac{\partial u_y(x_q, y_q)}{\partial y} \]

    \[ E_{xy} = E_{yx} = \frac{1}{2}( \frac{\partial u_x(x_q, y_q) }{\partial y} + \frac{\partial u_y(x_q, y_q)}{\partial x}). \]

    Therefore we have

    \[ E_{xx} = \sum_{i=1}^n\frac{\partial N_i(x_q, y_q)}{\partial x} u^i_x, \quad E_{yy} = \sum_{i=1}^n \frac{\partial N_i(x_q, y_q)}{\partial y} u^i_y \]

    \[ E_{xy} = E_{yx} = \frac{1}{2}( \sum_{i=1}^n \frac{\partial N_i(x_q, y_q) }{\partial y} u^i_x + \sum_{i=1}^n \frac{\partial N_i(x_q, y_q) }{\partial x} u^i_y). \]

  2. Out of plane component of strain is zero if it is plane-stress simulation. If it is plane-strain simulation then we use formula

    \[ E_{zz} = -\frac{\nu}{1 - \nu} (E_{xx} + E_{yy}).\]

  3. We use linear elastic constitutive equation to compute stress

    \[ \sigma_{xx} = \lambda (E_{xx} + E_{yy} + E_{zz}) + 2\mu E_{xx},\]

    \[\sigma_{yy} = \lambda (E_{xx} + E_{yy} + E_{zz}) + 2\mu E_{yy},\]

    \[ \sigma_{xy} = 2\mu E_{xy},\quad \sigma_{xz} = 2\mu E_{xz}, \quad \sigma_{yz} = 2\mu E_{yz}.\]

  4. If it is plane-strain, we have $ \sigma_{zz} = 0 $. Otherwise,

    \[ \sigma_{zz} = \nu (\sigma_{xx} + \sigma_{yy}) .\]

Parameters
writerPointer to vtk writer

Referenced by Compute().

Here is the caller graph for this function:

◆ decomposeSearchNodes()

void tools::pp::Compute::decomposeSearchNodes ( const std::pair< util::Point3, util::Point3 > &  cd,
std::vector< size_t > *  nodes,
std::vector< size_t > *  nodes_new 
)
private

Decompose node list into two lists.

We remove those nodes from the list which are outside the specified rectangle and add them to the new list.

Parameters
cdRectangle defined by two corner points
nodesPointer to ids of nodes
nodes_newPointer to new list of ids of nodes
Here is the call graph for this function:

◆ findCrackTip()

void tools::pp::Compute::findCrackTip ( std::vector< double > *  Z,
rw::writer::Writer *  writer 
)

Find crack tip location and velocity.

To compute the crack tip location at current output time, we first compute the damage at nodes. We then search for node which has smallest damage among nodes with damage above 1.

To compute crack tip velocity, we compare the tip at two different times . If not specified, then the two different times are the previous output time and current output time.

Since we compute damage in this method, we store the damage in global variable which can then be used in method computeDamage().

Parameters
ZPointer to nodal damage
writerPointer to vtk writer

Referenced by Compute().

Here is the caller graph for this function:

◆ findNode()

size_t tools::pp::Compute::findNode ( const util::Point3 &  x,
const std::vector< util::Point3 > *  nodes,
const std::vector< util::Point3 > *  u = nullptr 
)
private

Find node closest to given point.

If u is not null then given point is assumed to be in current configuration and therefore closest node in current configuration is searched.

Parameters
xPoint in reference/current configuration
nodesPointer to list of nodes
uPointer to nodal displacements
Returns
i Closest node to point x
Here is the call graph for this function:

◆ findTipInRects()

util::Point3 tools::pp::Compute::findTipInRects ( inp::EdgeCrack &  crack,
const double &  max_Z,
const std::vector< std::pair< util::Point3, util::Point3 >> &  rects,
const std::vector< std::vector< size_t >> &  nodes,
const std::vector< std::vector< double >> &  Zs,
const std::vector< double > *  Z,
bool  is_top 
)
private

Finds new crack tip location from the rectangle data.

In this method we implement Step 2 to 5 of Compute::updateCrack.

Parameters
crackCrack data
max_ZMaximum value of damage
rectsSequence of rectangles for search of new tip
nodesVector of nodal ids in rectangles
ZsVector of nodal damages in rectangles
ZPointer to nodal damage data
is_topTrue if searching for new tip for top side of crack
Returns
p New point
Here is the call graph for this function:

◆ getContourContribJInt()

void tools::pp::Compute::getContourContribJInt ( const util::Point3 &  p,
const std::vector< size_t > *  nodes,
const std::vector< size_t > *  elements,
const util::Point3 &  normal,
double &  pd_energy,
double &  kinetic_energy,
double &  elastic_energy,
util::Point3 &  dot_u,
bool  calc_in_ref,
const tools::pp::CrackTipData &  ctip 
)
private

Computes contribution to energy into crack from the quadrature point on contour.

Computes

\[ \frac{1}{2} \rho |\dot{u}(t)|^2 dt + \bar{W}(x; u(t)) \]

at given point, see computeJIntegral() for more details.

Parameters
pPoint
nodesPointer to ids of nodes to perform search
elementsPointer to ids of elements to perform search
normalNormal to the edge of contour
pd_energyPeridynamic energy density
kinetic_energyKinetic energy density
elastic_energyElastic energy density
dot_uMaterial velocity at the quadrature point
calc_in_refCalculate in reference configuration
ctipCurrent crack tip data
Here is the call graph for this function:

◆ getRectsAndNodesForCrackTip()

void tools::pp::Compute::getRectsAndNodesForCrackTip ( inp::EdgeCrack &  crack,
std::vector< std::pair< util::Point3, util::Point3 >> &  rects_t,
std::vector< std::pair< util::Point3, util::Point3 >> &  rects_b,
std::vector< std::vector< size_t >> &  nodes_t,
std::vector< std::vector< size_t >> &  nodes_b,
std::vector< std::vector< double >> &  Z_t,
std::vector< std::vector< double >> &  Z_b,
const std::vector< double > *  Z 
)
private

Creates sequence of rectangles for crack tip search, and finds the ids of nodes in each rectangle and damage associated to the node.

We filter out the nodes which have damage above max threshold and below min threshold defined in tools::pp::FindCrackTip.

Parameters
crackCrack data
rects_tSequence of rectangles for search of new top (right) tip
rects_bSequence of rectangles for search of new bottom (left) tip
nodes_tVector of nodal ids in rectangles for top (right) tip
nodes_bVector of nodal ids in rectangles for bottom (left) tip
Z_tVector of nodal damages in rectangles for top (right) tip
Z_bVector of nodal damages in rectangles for bottom (left) tip
ZPointer to nodal damage data
Here is the call graph for this function:

◆ initWriter()

void tools::pp::Compute::initWriter ( rw::writer::Writer *  writer,
std::vector< util::Point3 > *  u 
)

Create new writer object if it is not already done so.

Parameters
writerPointer to vtk writer
uPointer to nodal displacement vector

Referenced by Compute().

Here is the call graph for this function:
Here is the caller graph for this function:

◆ interpolateUV()

void tools::pp::Compute::interpolateUV ( const util::Point3 &  p,
util::Point3 &  up,
util::Point3 &  vp,
const std::vector< size_t > *  nodes,
const std::vector< size_t > *  elements,
bool  calc_in_ref 
)
private

Interpolates displacement and velocity at given point.

  1. For search over nodes/elements, we use list of nodes and elements which are created in listElemsAndNodesInDomain.
  2. If element-node connectivity is not available, this method uses piece-wise constant interpolation by searching for node closest to the point and assigning displacement and velocity of that node to the point.
  3. If element-node connectivity is available, then we find the element containing point. If element type is triangle then we use inverse mapping from given triangle to reference triangle to compute shape functions, see triCheckAndInterpolateUV.
  4. If element type is quadrangle, then we split quadrangle in two elements. Suppose $ v^1, v^2, v^3, v^4 $ are vertices of quadrangle, then we consider triangle $ T_1 = (v^1, v^2, v^3) $ and $ T_2 = (v^1, v^3, v^4) $ and find if point belongs to $ T_1 $ or $ T_2 $ and proceed similar to the case of triangle element (see triCheckAndInterpolateUV).
Parameters
pPoint at which we want to interpolate
upDisplacement at the point p
vpVelocity at the point p
nodesPointer to ids of nodes to perform search
elementsPointer to ids of elements to perform search
calc_in_refCalculate in reference configuration
Here is the call graph for this function:

◆ listElemsAndNodesInDomain()

void tools::pp::Compute::listElemsAndNodesInDomain ( const std::pair< util::Point3, util::Point3 > &  cd,
const double &  tol,
const double &  tol_elem,
std::vector< size_t > *  nodes,
std::vector< size_t > *  elements,
bool  calc_in_ref 
)
private

Find node within contour and elements intersecting contour.

For nodes list, we consider domain which envelopes contour. Thickness of domain is typically taken as size of horizon + 2 * mesh size.

For element list, we look for element which has at least 1 node in the domain enveloping contour. The thickness of domain is typically taken as mesh size.

Parameters
cdRectangle defining the contour
tolThickness for node list search
tol_elemThickness for element list search
nodesPointer to ids of nodes
elementsPointer to ids of elements
calc_in_refCalculate in reference configuration
Here is the call graph for this function:

◆ readComputeInstruction()

void tools::pp::Compute::readComputeInstruction ( const std::string &  set,
tools::pp::InstructionData *  data 
)

Read compute instruction.

Parameters
setTag for given compute set
dataPointer to instruction data

◆ readCrackTipData()

void tools::pp::Compute::readCrackTipData ( const std::string &  filename,
int  crack_id,
std::vector< tools::pp::CrackTipData > *  data,
bool  is_inclined = false 
)

Read crack tip data.

Parameters
filenameFilename to read crack tip data
crack_idId of crack to read
dataPointer to data where crack tip data will be stored

◆ safeExit()

void tools::pp::Compute::safeExit ( const std::string &  err_message,
rw::writer::Writer *  writer = nullptr 
)
private

Exits code safely in the event there is error.

Parameters
err_messageError message
writerWriter object
Here is the call graph for this function:

◆ transformU()

void tools::pp::Compute::transformU ( rw::writer::Writer *  writer)

Transform displacement.

Currently following transformation is implemented

  • Scale displacement by specified factor
Parameters
writerPointer to vtk writer

Referenced by Compute().

Here is the call graph for this function:
Here is the caller graph for this function:

◆ transformV()

void tools::pp::Compute::transformV ( rw::writer::Writer *  writer)

Transform velocity.

There are two transformation implemented

  • Mark velocity of certain nodes as zero
  • Symmetric the velocity field
Parameters
writerPointer to vtk writer

Referenced by Compute().

Here is the call graph for this function:
Here is the caller graph for this function:

◆ triCheckAndInterpolateUV()

bool tools::pp::Compute::triCheckAndInterpolateUV ( const util::Point3 &  p,
util::Point3 &  up,
util::Point3 &  vp,
const std::vector< size_t > &  ids,
bool  calc_in_ref,
bool  check_only = false 
)
private

Interpolates displacement and velocity at given point in triangle.

Triangle is specified by global ids of nodes. We first check if point is within the triangle $ T $. If yes then we use TriElem::getShapes to compute the shape functions $ N_1, N_2, N_3 $ at the given point. Using shape function we can interpolate displacement and velocity as follows:

\[ u = \sum_{i=1}^3 N_i u^i, \quad v = \sum_{i=1}^3 N_i v^i \]

where $ u^i, v^i $ are displacement and velocity of vertex $ i $ of triangle.

Parameters
pPoint at which we want to interpolate
upDisplacement at the point p
vpVelocity at the point p
idsGlobal ids of vertices of triangle
calc_in_refCalculate in reference configuration
check_onlyTrue if only interested in whether the point belongs to triangle
Returns
status True if point is found in the triangle. Otherwise false.
Here is the call graph for this function:

◆ updateCrack()

void tools::pp::Compute::updateCrack ( const double &  time,
const std::vector< double > *  Z 
)
private

Updates crack tip location and crack velocity.

Method:

  • Step 1 - We consider sequence of rectangle starting from the tip of crack towards the end of material domain and find the ids and damage of nodes within each of these rectangles. We skip the nodes which have damage above specified bound (say 50) and below specified bound (say 1).
  • Step 2 - We find the minimum value of damage among nodes in each rectangle and sort the rectangle by increasing order of minimum damage. This way we attach two data to each rectangle in sequence of rectangle: minimum damage and the node which has that damage. Once we sort the rectangle in increasing order of damage associated to it, we take first and second rectangle as best choice of rectangle and find suitable crack tip in these two rectangles.
  • Step 3 - In first and second rectangle (after sorting in step 2) we find the node which has closest damage to the minimum damage in both these rectangle and which is also closest to the crack line defined by the old crack tip. If we find the node which has damage closer to the minimum and is more closer to the crack line, we update the damage and node of rectangle by the damage of new found node and id of new found node.
  • Step 4 - For rectangle 1 and 2, we now search for node which has damage very close to the damage associated to the rectangle and which is located opposite to the crack line. First choice of crack line is initial crack line, second choice is crack line given by old crack tip, and third choice is crack line given by current crack tip. There are three possibilities
    1. Rectangle 1 has symmetrically opposite node
    2. Rectangle 1 does not have symmetrically opposite node and rectangle 2 has symmetrically opposite node
    3. Rectangle 1 and 2 both do not have symmetrically opposite node
  • Step 5 - We find crack tip from rectangle 1 if it is either case 1 or 3. In case of 2 we find crack tip from rectangle 2. We use average of two points in case of 1 and 2, and use average of nodal position of node associated to rectangle 1 and current crack tip to define new crack tip.

Step 2 - 5 is implemented in Compute::findTipInRects.

Parameters
timeCurrent time
ZVector of damage at nodes
Here is the call graph for this function:

Field Documentation

◆ d_dtOutChange

size_t tools::pp::Compute::d_dtOutChange
private

Time step at which output interval changes.

Since we now support criteria based output intervals, we need to know when the transition from one interval to another happens. See model::FDModel::checkOutputCriteria() for details about the criteria based output intervals.

Default value is total number of simulation steps. For this value, we always read output files which correspond to time steps in the interval Dt, where Dt is maximum of two intervals in the simulation input file.

Referenced by Compute().

◆ d_input_p

inp::Input* tools::pp::Compute::d_input_p
private

Pointer to Fracture object.

Pointer to Input object

Referenced by Compute().

◆ d_mX

std::vector<double> tools::pp::Compute::d_mX
private

Weighted volume.

In case of Rob's state based model, this data is not required

◆ d_outputDeck_p

inp::OutputDeck* tools::pp::Compute::d_outputDeck_p
private

Model deck.

Output deck

Referenced by Compute().

◆ d_simInpFilename

std::string tools::pp::Compute::d_simInpFilename
private

Simulation input filename.

This filename is same input file used in running simulation

◆ d_thetaX

std::vector<double> tools::pp::Compute::d_thetaX
private

Dilation.

In case of Rob's state based model, this will give the spherical (hydrostatic) strain

The documentation for this class was generated from the following files: