 |
NLMech
0.1.0
|
 |
NLMech
0.1.0
|
A Class implementing regularized nonlinear peridynamic model. More...
#include <rnpBond.h>
Public Member Functions | |
| std::pair< util::Point3, double > | getBondEF (size_t i, size_t j) |
| Returns energy and force state between node i and node j. More... | |
| util::Point3 | getBondForceDirection (const util::Point3 &dx, const util::Point3 &du) const |
| Get direction of bond force. More... | |
| double | getInfFn (const double &r) const |
| Returns the value of influence function. More... | |
| double | getS (const util::Point3 &dx, const util::Point3 &du) |
| Returns the bond strain. More... | |
| double | getS (size_t i, size_t j) |
| Returns the bond strain. More... | |
| double | getSc (const double &r) |
| Returns critical bond strain. More... | |
| double | getSc (size_t i, size_t j) |
| Returns critical bond strain. More... | |
| RNPBond (inp::MaterialDeck *deck, data::DataManager *dataManager) | |
| Constructor. More... | |
 Public Member Functions inherited from material::pd::BaseMaterial Public Member Functions inherited from material::pd::BaseMaterial | |
| BaseMaterial (const size_t &dim, const double &horizon) | |
| Constructor. More... | |
| double | getDensity () const |
| Returns the density of the material. More... | |
| double | getHorizon () const |
| Returns horizon. More... | |
| virtual util::Matrix33 | getStrain (size_t i) |
| Returns strain tensor. More... | |
| virtual util::Matrix33 | getStress (size_t i) |
| Returns stress tensor. More... | |
| bool | isStateActive () const |
| Returns true if state-based potential is active. More... | |
| std::string | name () const |
| Returns name of the material. More... | |
| virtual void | print (int nt=0, int lvl=0) const |
| Prints the information about the instance of the object. More... | |
| virtual std::string | printStr (int nt=0, int lvl=0) const |
| Returns the string containing information about the instance of the object. More... | |
| virtual void | update () |
| Let the material class in the quasi-static case know that there is a new loading step. | |
Private Member Functions | |
| void | computeMaterialProperties (inp::MaterialDeck *deck, const double &M) |
| Computes elastic and fracture properties from the rnp material parameters. More... | |
| void | computeParameters (inp::MaterialDeck *deck, const double &M) |
| Computes rnp material parameters from elastic constants. More... | |
Private Attributes | |
| material::pd::BaseInfluenceFn * | d_baseInfluenceFn_p |
| Base object for influence function. | |
| double | d_contact_Kn = 0. |
| Kn coefficient for normal contact force between broken bonds. | |
| double | d_contact_Rc = 0. |
| Contact radius for normal contact force between broken bonds. | |
| data::DataManager * | d_dataManager_p |
| Store pointer to datamanager. | |
| const inp::MaterialDeck * | d_deck |
| Pointer to the material deck. | |
| double | d_factorSc |
| Factor to multiply to critical strain to check if bond is fractured. More... | |
| double | d_invFactor |
Inverse of factor =  . . | |
| bool | d_irrevBondBreak |
| Flag which indicates if the breaking of bond is irreversible. | |
| double | d_rbar |
Inflection point of nonlinear function =  . . | |
Material parameters | |
| double | d_C |
| Parameter C. | |
| double | d_beta |
Parameter  . . | |
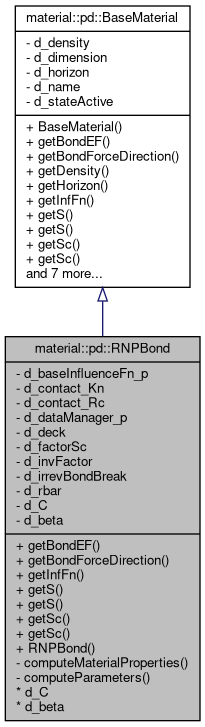
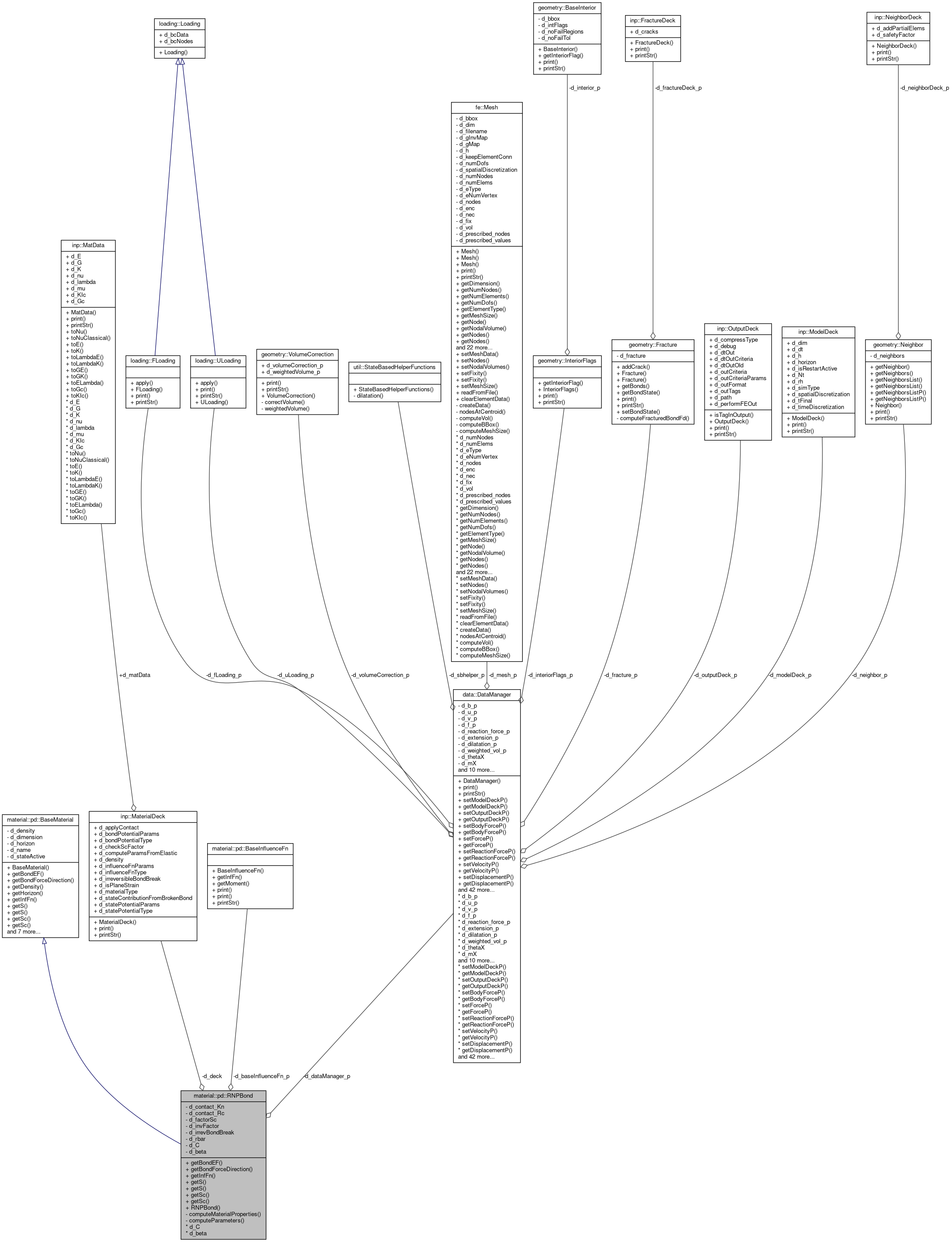
A Class implementing regularized nonlinear peridynamic model.
Provides method to compute energy and force using nonlinear bond-based model introduced and studied in Lipton 2016, Jha and Lipton 2018, and Lipton and Jha 2019.
![\[ E_{bond} = \int_D \frac{1}{|B_\epsilon(x)|} \int_{B_\epsilon(x)} |y-x| W_{bond}(S(y,x; u)) dy dx \]](form_224.png)
 is a ball (circle in 2-d) centered at
is a ball (circle in 2-d) centered at  of radius
of radius  ,
,  is the volume (area in 2-d) of ball,
is the volume (area in 2-d) of ball,  is the linearized bond strain (assuming small deformation).
is the linearized bond strain (assuming small deformation). is given by
is given by
![\[ W_{bond} (S(y,x;u)) = J^\epsilon(|y-x|) \frac{1}{\epsilon |y-x|} \psi (|y-x| S(y,x;u)^2) \]](form_230.png)
 is positive, smooth, concave function with following properties
is positive, smooth, concave function with following properties
![\[ \lim_{r\to 0^+} \frac{\psi(r)}{r} = \psi'(0), \quad \lim_{r\to \infty} \psi(r) = \psi_\infty < \infty. \]](form_232.png)
 is the influence function.
is the influence function. is given by
is given by
![\[ f_{bond}(x) = \frac{4}{|B_\epsilon(x)|} \int_{B_\epsilon(x)} \frac{J^\epsilon(|y-x|)}{\epsilon} \psi'(|y-x| S(y,x;u)^2) S(y,x;u) \frac{y-x}{|y-x|} dy.\]](form_235.png)
![\[ \psi(r) = C ( 1-\exp[-\beta r] \]](form_236.png)
 are the peridynamic material parameter determined from the elastic and fracture properties of the material.
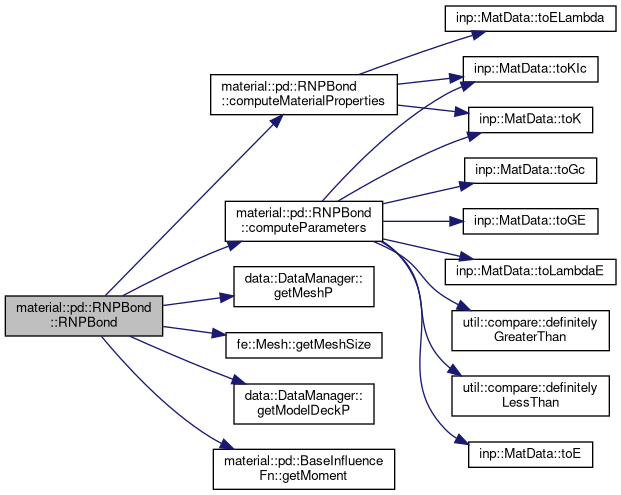
are the peridynamic material parameter determined from the elastic and fracture properties of the material. | material::pd::RNPBond::RNPBond | ( | inp::MaterialDeck * | deck, |
| data::DataManager * | dataManager | ||
| ) |
Constructor.
| deck | Pointer to the input deck |
| DataManager | Pointer to the data manager object |
|
private |
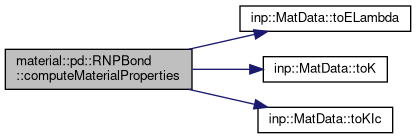
Computes elastic and fracture properties from the rnp material parameters.
This function does opposite of pd::Material::RNPBond::computeParameters. From peridynamic material properties, it uses the relation between lame parameters and peridynamic parameters to compute the lame parameters, and from lame parameters it computes the elastic constants.
| deck | Input material deck |
| M | Moment of influence function |
Referenced by RNPBond().

|
private |
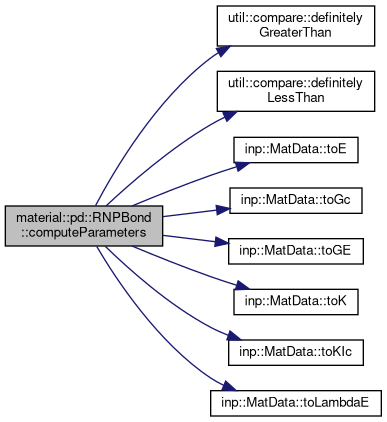
Computes rnp material parameters from elastic constants.
Either Young's modulus E or bulk modulus K, and either critical energy release rate Gc or critical stress intensity factor KIc are needed. Assuming Poisson's ratio  we compute lame parameters
we compute lame parameters  where
where  for bond-based.
for bond-based.
With lame parameters, we use following formula, see Equation (5.7) & (5 .8) of Lipton 2016

![\[ \lambda = \mu = \frac{\psi'(0)}{4} M_2, \qquad Gc = \frac{4 \psi_{\infty}}{\pi} M_2. \]](form_242.png)

![\[ \lambda = \mu = \frac{\psi'(0)}{5} M_3, \qquad Gc = \frac{3 \psi_{\infty}}{2} M_3. \]](form_244.png)
Where  are defined by
are defined by
![\[ M_2 =\int_0^1 r^2 J(r) dr, \qquad M_3 = \int_0^1 r^3 J(r) dr. \]](form_246.png)
For potential function ![$ \psi(r) = c ( 1-\exp[-\beta r])$](form_247.png) , we have
, we have  . Thus, the values of
. Thus, the values of  are given by
are given by

![\[ c = \frac{\pi G_c}{4} \frac{1}{M_2}, \qquad \beta = \frac{4 \lambda}{c} \frac{1}{M_2} .\]](form_250.png)

![\[ c = \frac{2 G_c}{3} \frac{1}{M_3}, \qquad \beta = \frac{5 \lambda}{c} \frac{1}{M_3} .\]](form_252.png)
| deck | Input material deck |
| M | Moment of influence function |
Referenced by RNPBond().

|
virtual |
Returns energy and force state between node i and node j.
| i | Id of node i |
| j | node of j |
Reimplemented from material::pd::BaseMaterial.

|
virtual |
Get direction of bond force.
| dx | Relative bond vector (reference configuration) |
| du | Relative bond displacement vector |
Reimplemented from material::pd::BaseMaterial.

|
virtual |
Returns the value of influence function.
| r | Reference (initial) bond length |
Reimplemented from material::pd::BaseMaterial.
|
virtual |
Returns the bond strain.
| dx | Reference bond vector |
| du | Difference of displacement |
Reimplemented from material::pd::BaseMaterial.

|
virtual |
Returns the bond strain.
| i | Id of node 1 |
| j | Id of node 2 |
Reimplemented from material::pd::BaseMaterial.
|
virtual |
Returns critical bond strain.
| r | Reference length of bond |
Reimplemented from material::pd::BaseMaterial.
|
virtual |
Returns critical bond strain.
| i | Id of node 1 |
| j | Id of node 2 |
Reimplemented from material::pd::BaseMaterial.
|
private |
Factor to multiply to critical strain to check if bond is fractured.
For nonlinear model, we consider bond is broken when it exceeds 10 times of critical strain. Typical value of factor is 10.
Referenced by RNPBond().